Diffusion Equation in Python

Diffusion Equation in Python | In this article, we will discuss the diffusion equation and how we can solve it using Python programming. So, firstly we must know what the diffusion equation is.

The diffusion equation is a partial differential equation that describes how a quantity (such as heat or mass) diffuses through a medium. In this article, we’ll explore how to solve the diffusion equation in Python using the finite difference method.

What is Diffusion Equation?

The diffusion equation is a second-order partial differential equation that describes the evolution of a quantity $u(x,t)$ in space $x$ and time $t$. It can be written as:-

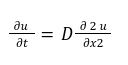
Where $D$ is the diffusion coefficient. This equation states that the rate of change of $u$ with respect to time is proportional to the second derivative of $u$ with respect to space.

Solving the Diffusion Equation in Python

Let’s now write some Python code to solve the diffusion equation using the finite difference method. We’ll start by defining some parameters:-

import numpy as np
import matplotlib.pyplot as plt

# Define parameters
L = 1.0  # Length of domain
nx = 100  # Number of grid points
dx = L / (nx - 1)  # Grid spacing
nt = 1000  # Number of time steps
dt = 0.001  # Time step size
D = 1.0  # Diffusion coefficient

Here, we’ve defined the length of the domain ‘L’, the number of grid points ‘nx’, the grid spacing ‘dx’, the number of time steps ‘nt’, the time step size ‘dt’, and the diffusion coefficient ‘D’. Next, we’ll set the initial condition for ‘$u$’:-

# Set initial condition
u0 = np.zeros(nx)
u0[int(0.4 / dx) : int(0.6 / dx)] = 1.0

Here, we’ve set the initial condition to be a rectangular pulse with a width of 0.2 units centered around the point x = 0.5.

Now, we’ll iterate over time steps using the finite difference equation:-

# Iterate over time steps
u = u0.copy()
for n in range(nt):
    un = u.copy()
    for i in range(1, nx - 1):
        u[i] = un[i] + D * dt / dx**2 * (un[i + 1] - 2 * un[i] + un[i - 1])

Here, we’re iterating over time steps using a nested loop. In the outer loop, we’re iterating over time.

1D Diffusion Equation in Python

Here’s an example of how to solve the 1D diffusion equation in Python using the finite difference method:-

import numpy as np
import matplotlib.pyplot as plt

# Define parameters
L = 1.0  # Length of domain
nx = 100  # Number of grid points
dx = L / (nx - 1)  # Grid spacing
nt = 1000  # Number of time steps
dt = 0.001  # Time step size
D = 1.0  # Diffusion coefficient

# Set initial condition
u0 = np.zeros(nx)
u0[int(0.4 / dx) : int(0.6 / dx)] = 1.0

# Iterate over time steps
u = u0.copy()
for n in range(nt):
    un = u.copy()
    for i in range(1, nx - 1):
        u[i] = un[i] + D * dt / dx**2 * (un[i + 1] - 2 * un[i] + un[i - 1])

# Plot solution
x = np.linspace(0, L, nx)
plt.plot(x, u)
plt.xlabel("x")
plt.ylabel("u")
plt.show()

Here, we’ve defined the same parameters as in the previous example, except we’ve reduced the number of dimensions to 1. We’ve also set the initial condition to be a rectangular pulse centered around the point x = 0.5.

The main difference in the code is the nested loop that iterates over time steps and grid points. In each iteration, we’re updating the value of $u$ at each grid point using the finite difference equation:-

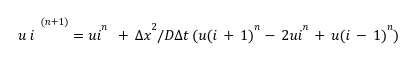
Where $i$ is the grid point index and $n$ is the time step index. Finally, we plot the solution using Matplotlib. The resulting plot shows how the rectangular pulse diffuses over time due to the diffusion coefficient $D$.

1D Diffusion Equation in Python

Here’s an example of how to solve the 2D diffusion equation in Python using the finite difference method:-

import numpy as np
import matplotlib.pyplot as plt

# Define parameters
L = 1.0  # Length of domain
nx = 100  # Number of grid points in x direction
ny = 100  # Number of grid points in y direction
dx = L / (nx - 1)  # Grid spacing in x direction
dy = L / (ny - 1)  # Grid spacing in y direction
nt = 1000  # Number of time steps
dt = 0.001  # Time step size
D = 1.0  # Diffusion coefficient

# Set initial condition
u0 = np.zeros((ny, nx))
u0[int(0.4 / dy) : int(0.6 / dy), int(0.4 / dx) : int(0.6 / dx)] = 1.0

# Iterate over time steps
u = u0.copy()
for n in range(nt):
    un = u.copy()
    for i in range(1, ny - 1):
        for j in range(1, nx - 1):
            u[i, j] = (
                un[i, j]
                + D * dt / dx**2 * (un[i, j + 1] - 2 * un[i, j] + un[i, j - 1])
                + D * dt / dy**2 * (un[i + 1, j] - 2 * un[i, j] + un[i - 1, j])
            )

# Plot solution
x = np.linspace(0, L, nx)
y = np.linspace(0, L, ny)
X, Y = np.meshgrid(x, y)
plt.contourf(X, Y, u)
plt.colorbar()
plt.xlabel("x")
plt.ylabel("y")
plt.show()

Here, we’ve defined a 2D domain with ‘nx’ grid points in the ‘x direction’ and ‘ny’ grid points in the ‘y direction’. We’ve also set the initial condition to be a rectangular pulse centered around the point (0.5, 0.5).

The main difference in the code is the nested loops that iterate over time steps and grid points in both the x and y directions. In each iteration, we’re updating the value of $u$ at each grid point using the finite difference equation:-

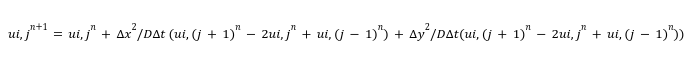
Where $i$ and $j$ are the grid point indices in the x and y directions, respectively, and $n$ is the time step index.

Finally, we plot the solution using Matplotlib. The resulting plot shows how the rectangular pulse diffuses over time due to the diffusion coefficient $D$. The “contourf” function is used to create a filled contour plot of the solution, with a colorbar to indicate the values of $u$.

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!

Search