Tree Data Structure - Know Program

Tree Data Structure | Tree is a non-linear data structure. A tree data structure is a widely used hierarchical data structure that mimics a tree’s natural structure. Here’s a comprehensive overview.

Table of Contents

Key Concepts:-

        A
       /|\
      B C D
     /|   |\
    E F   G H

Nodes: Each element in the tree is called a node. Example:- A, B, C, D, E, F, G, H.
Root: The top node is called the root. It has no parent. Example:- A.
Edges: The connections between nodes are called edges.
Parent and Child: Each node, except the root, has exactly one parent. Nodes that share the same parent are called siblings. Nodes that are directly connected from a node are called children. (e.g., A is the parent of B, C, and D. B, C, and D are siblings).
Leaf: A node with no children is called a leaf or terminal node. Example: C, E, F, G, H
Subtree: A subtree is a tree consisting of a node and its descendants. Example: Subtree rooted at B includes B, E, and F.
Descendants: Descendants of a node are all nodes that are reachable from that node by moving downwards in the tree. Descendants of B are E and F.
Ancestors: Ancestors of a node are all nodes that are reachable from that node by moving upwards in the tree. Ancestors of F are B and A.
Degree: The degree of a node is the number of children the node has. The degree of a tree is the maximum degree of any node in the tree. Example: Degree of A is 3 (since it has three children: B, C, and D). The maximum degree in this tree is 3, which is the degree of node A.
Internal Node: Nodes that are not leaf nodes are called internal nodes. Example: A, B, D.

Tree Properties:

Height: The height of a node is the number of edges on the longest path from the node to a leaf. The height of a tree is the height of the root node.
Depth: The depth of a node is the number of edges from the root to the node. The depth of the root node is 0.
Level: The level of a node is the depth of the node plus one. The root node is at level 1.
Degree: The degree of a node is the number of children it has. The degree of a tree is the maximum degree of its nodes.

Types of Trees:

Binary Tree: Each node has at most two children, referred to as the left child and the right child.
Binary Search Tree (BST): A binary tree where for each node, the left child’s value is less than the node’s value, and the right child’s value is greater.
Balanced Tree: A tree where the height of the left and right subtrees of any node differ by no more than one.
AVL Tree: A self-balancing binary search tree where the difference in heights between the left and right subtrees is at most one.
B-Tree: A self-balancing search tree in which nodes can have more than two children, widely used in databases and file systems.
Trie: Also known as a prefix tree, used for efficient retrieval of a key in a large dataset of strings.
Heap: A complete binary tree where the value of each node is either greater than or equal to (max-heap) or less than or equal to (min-heap) the values of its children.

Common Operations:

Insertion: Adding a node to the tree.
Deletion: Removing a node from the tree.
Traversal: Visiting all the nodes in a specific order. Common traversal methods include:
- Preorder: Visit the root, traverse the left subtree, traverse the right subtree.
- Inorder: Traverse the left subtree, visit the root, and traverse the right subtree.
- Postorder: Traverse the left subtree, traverse the right subtree, and visit the root.
- Level-order: Visit nodes level by level from left to right.

Applications of Tree Data Structures

Hierarchical Data Representation:
- Organization Structure: Represents company hierarchies with employees and departments.
- Folder Structure: Manages directories and files in filesystems.
- XML/HTML Content: Structures nested tags in documents.
- OOP (Inheritance): Represents class hierarchies.
Binary Search Trees (BSTs): Efficiently supports searching, insertion, and deletion operations.
Binary Heap: Implements priority queues for process scheduling and algorithms like Dijkstra’s.
B and B+ Trees in DBMS: Manages large datasets in databases for efficient retrieval and storage.
Spanning and Shortcut Path Trees in computer networks: Spanning Trees prevent loops in network topologies. Shortest Path Trees find efficient routes between nodes.
Parse Tree, Expression Tree in Compilers: Parse Trees represent syntactic structures of programming languages. Expression Trees facilitate arithmetic expression evaluations and optimizations.

Variations of Tree

Trie: A tree used for efficient retrieval of a key in a large dataset of strings, often used in autocomplete and spell-checking.
Suffix Tree: A compressed trie containing all suffixes of a given text, used for string matching problems and finding longest repeated substrings.
Binary Index Tree: Also known as Fenwick Tree, it provides efficient methods for calculation and manipulation of prefix sums, useful in scenarios requiring dynamic cumulative frequency tables.
Segment Tree: A tree used for storing intervals or segments, allowing efficient querying and updating of ranges, commonly used in computational geometry and solving range query problems.

Binary Tree

Every node has at most two children. Binary trees are fundamental in computer science, often used to implement efficient searching and sorting algorithms.

        30
       / \
      40  50
     /    / \
    70   60  80

Every node contains:- left pointer, right pointer, and data. The left pointer refer to left child, and right pointer refer to the right child. For leaf node the left and right pointers are null.

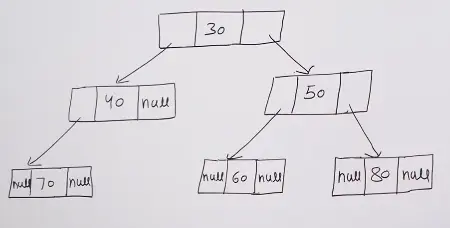
Most of the popular and practically used tree data structure are variation of Binary Tree. Therefore we mostly study Binary Tree in academics.

class Node {
    int key;
    Node left;
    Node right;

    Node(int k) {
        key = k;
    }
}

public class Test {
    public static void main(String[] args) {
        Node root = new Node(10);
        root.left = new Node(20);
        root.right = new Node(30);
        root.left.left = new Node(40);
        root.left.right = new Node(50);
    }
}

Tree Structure:-

Tree Traversal

Types of Tree Traversal:

Breadth-First (Level Order): Visits all nodes at the present depth level before moving on to nodes at the next depth level. Example:- 10, 20, 30, 40, 50. Top to bottom and left to right.
Depth-First:
- Preorder: Visits the root node, then the left subtree, and finally the right subtree. (root, left, right).
- Inorder: Visits the left subtree, the root node, and then the right subtree. (left, root, right).
- Postorder: Visits the left subtree, the right subtree, and then the root node. (left, right, root).

        10
       /  \
      20  30

Preorder: 10 20 30
Inorder: 20 10 30
Postorder: 20 30 10

         10
       /    \
      20     30
     / \      / 
    40  50   60
        / \
       70  80

Preorder: 10 20 40 50 70 80 30 60
Inorder: 40 20 70 50 80 10 30 60
Postorder: 40 70 80 50 20 60 30 10

Let us implement inorder, preorder, and postorder traversal for the below tree:-


public class BinaryTree {
    Node root;

    public static void main(String[] args) {
        BinaryTree bt = new BinaryTree();
        bt.root = new Node(10);
        bt.root.left = new Node(20);
        bt.root.right = new Node(30);
        bt.root.right.left = new Node(40);
        bt.root.right.right = new Node(50);

        // bt.preorder(bt.root);
        System.out.println();

        // bt.inorder(bt.root);
        System.out.println();

        // bt.postorder(bt.root);
    }
}

class Node {
    Node left;
    int key;
    Node right;

    public Node(int key) {
        this.key = key;
    }
}

Preorder Traversal

// root => left => right
void preorder(Node node) {
    if (node != null) {
        System.out.print(node.key + " ");
        preorder(node.left);
        preorder(node.right);
    }
}

Output:- 10 20 30 40 50

Inorder Traversal

// left => root => right
void inorder(Node node) {
    if (node != null) {
        inorder(node.left);
        System.out.print(node.key + " ");
        inorder(node.right);
    }
}

Output:- 20 10 40 30 50

Postorder Traversal

// left => right => root
void postorder(Node node) {
    if (node != null) {
        postorder(node.left);
        postorder(node.right);
        System.out.print(node.key + " ");
    }
}

Output:- 20 40 50 30 10

For all these 3 traversals:-
Time complexity: O(n)
Auxiliary space: O(h)

Comparison:-

Inorder: Best for sorting and BST validation.
Preorder: Best for tree copying and hierarchical data export.
Postorder: Best for tree deletion and resource management.

In tree, pre-order traversal, and in-order traversal are tail-recursive whereas post-order traversal is non-tail recursive. Therefore pre-order traversal and in-order traversal are preferred over post-order traversal.

1. Height of Binary Tree

For a given Binary Tree, find the height. The height of a binary tree is the maximum number of nodes from the root to the leaf node. Problem: 104

I/P: 10, O/P: 1
I/P: null, O/P: 0
I/P:

O/P: 4

The below method calculates the height of a binary tree by recursively determining the height of the left and right subtrees and taking the maximum of the two, then adding one to account for the current node.

private int height(Node node) {
    if (node == null) {
        return 0;
    }
    return Math.max(height(node.left), 
                    height(node.right)) 
           + 1;
}

Time complexity: O(n), Auxiliary Space: O(h)

2. Print Nodes at Distance K

        10
       /  \
      20   30
     / \    \
    40  50   70
              \
              80

k = 2
Output: 40 50 70

void printAtKDist(Node node, int k) {
    if (node == null) {
        return;
    }
    if (k == 0) {
        System.out.print(node.key + " ");
        return;
    }
    printAtKDist(node.left, k - 1);
    printAtKDist(node.right, k - 1);
}

Time complexity: O(n), Auxiliary Space: O(h)

3. Level Order Traversal or Breadth First Search (BFS)

Traversal order: Left to right and Top to bottom.

         10         -- Level 1
       /    \
      20     30     -- Level 2
     / \       \ 
    40  50     60   -- Level 3
        / \
       70  80       -- Level 4

Output: 10 20 30 40 50 60 70 80

public class BinaryTree {
    Node root;

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(10);
        tree.root.left = new Node(20);
        tree.root.right = new Node(30);
        tree.root.right.right = new Node(60);
        tree.root.left.left = new Node(40);
        tree.root.left.right = new Node(50);
        tree.root.left.right.left = new Node(70);
        tree.root.left.right.right = new Node(80);

        tree.levelOrder(tree.root);
    }

    private void levelOrder(Node node) {
        // TODO
    }
}

One way is to define a method to find the distance of the binary tree and define another method to print elements at distance k. It is not an efficient solution. It will have time complexity O(n*h), but we want to do it in O(n). We can use the queue data structure for this purpose.

private void levelOrder(Node node) {
    if (node == null) {
        return;
    }
    
    Queue<Node> q = new LinkedList<>();
    q.offer(node);
    
    while (!q.isEmpty()) {
        Node curr = q.poll();
        System.out.print(curr.key + " ");
        
        if (curr.left != null) {
            q.offer(curr.left);
        }
        
        if (curr.right != null) {
            q.offer(curr.right);
        }
    }
}

Every node goes to the queue exactly once and comes out of the queue exactly once. Therefore the Time complexity: O(n), Auxiliary Space: O(n). In general, we can say that the auxiliary space required for the level order traversal of the binary tree is Θ(w) where w is the width of the binary tree.

4. Level Order Traversal Line by Line

After each level traversal print a line. Problem: 102.

         10         -- Level 1
       /    \
      20     30     -- Level 2
     / \       \ 
    40  50     60   -- Level 3
        / \
       70  80       -- Level 4

Output:-
10
20 30
40 50 60
70 80

Idea: When we traverse the last node of the level then put null in the queue. So whenever we see null it means we have reached the level’s end and can push another null.

private void levelOrderLByL(Node node) {
    if (node == null) {
        return;
    }

    Queue<Node> q = new LinkedList<>();
    q.offer(node);
    q.offer(null); // added null to mark the end of the current level

    while (q.size() > 1) {
        Node curr = q.poll();

        if (curr == null) {
            System.out.println();
            q.offer(null);
            continue;
        }

        System.out.print(curr.key + " ");

        if (curr.left != null) {
            q.offer(curr.left);
        }

        if (curr.right != null) {
            q.offer(curr.right);
        }
    }
}

Time complexity: O(n), Auxiliary Space: O(n) or Θ(width).

Method-2:- In the previous approach, we added null after each level traversal, but now we will break down the level order traversal into 2 loops. The inner loop prints 1 level at a time and the outer loop prints a new line. We will use the size of the queue.

private void levelOrderLByL(Node node) {
    if (node == null) {
        return;
    }

    Queue<Node> q = new LinkedList<>();
    q.offer(node);

    while (!q.isEmpty()) {
        // Queue size will change
        // therefore take a copy of current size
        int count = q.size();

        for (int i = 0; i < count; i++) {
            Node curr = q.poll();
            System.out.print(curr.key + " ");

            if (curr.left != null) {
                q.offer(curr.left);
            }

            if (curr.right != null) {
                q.offer(curr.right);
            }
        }

        System.out.println();
    }
}

Each node will enter into the queue exactly once and come out of the queue exactly once therefore time complexity is O(n). Auxiliary Space: O(n) or Θ(width).

5. Size of a Binary Tree

         10
       /    \
      20     30
     / \       \ 
    40  50     60
        / \
       70  80

We have to count the number of nodes in the binary tree. For example in the above tree size = 8.

// recursive
private int size(Node node) {
    if (node == null) {
        return 0;
    }
    return 1 + size(node.left) + size(node.right);
}

Time complexity: O(n), Auxiliary Space: O(h)

// iterative
private int size(Node node) {
    if (node == null) {
        return 0;
    }

    Queue<Node> q = new LinkedList<>();
    q.offer(node);
    int count = 1;

    while (!q.isEmpty()) {
        Node curr = q.poll();

        if (curr.left != null) {
            q.offer(curr.left);
            count++;
        }

        if (curr.right != null) {
            q.offer(curr.right);
            count++;
        }
    }

    return count;
}

Time complexity: O(n), Auxiliary Space: O(width)

6. Maximum in Binary Tree

Find the maximum value in Binary Tree. If the root is null then return -Infinity.

// recrusive
private int getMax(Node node) {
    if (node == null) {
        return Integer.MIN_VALUE;
    }
    return Math.max(node.key, 
       Math.max(getMax(node.left), getMax(node.right)));
}

Time complexity: O(n), Auxiliary Space: O(h)

// iterative
private int getMax(Node node) {
    if (node == null) {
        return 0;
    }

    Queue<Node> q = new LinkedList<>();
    q.offer(node);
    int max = Integer.MIN_VALUE;

    while (!q.isEmpty()) {
        Node curr = q.poll();
        max = Math.max(max, curr.key);

        if (curr.left != null) {
            q.offer(curr.left);
        }

        if (curr.right != null) {
            q.offer(curr.right);
        }
    }

    return max;
}

Time complexity: O(n), Auxiliary Space: O(width)

7. Print Left View of Binary Tree

The left view of a binary tree includes all the nodes that are visible when the tree is viewed from the left side. At every level print the leftmost node.

     10
    /  \
   20   30
  /  \    \
 40  50   60

Left View: 10 20 40

Left View: 30 50 60 10

Left View: 10 50 70 8

Iterative approach: It is based on the line by line level order traversal. After each line, print only the first item.

private void leftView(Node node) {
    if (node == null) {
        return;
    }

    Queue<Node> q = new LinkedList<>();
    q.offer(node);

    while (!q.isEmpty()) {
        int size = q.size();

        for (int i = 0; i < size; i++) {
            Node curr = q.poll();

            if (i == 0) {
                System.out.print(curr.key + " ");
            }

            if (curr.left != null) {
                q.offer(curr.left);
            }

            if (curr.right != null) {
                q.offer(curr.right);
            }
        }
    }
}

Time complexity is O(n). Auxiliary Space: O(n) or Θ(width).

Recursive Method:- If we do preorder traversal then we will always travel to the leftmost node before any other node. Do preorder traversal and maintain 2 extra variables:- maxLevel (level which we have already traveled; initialized as 0), level (current level, initialized as 1). At any node, we check level > maxLevel. If level > maxLevel it means it is the leftmost node of its level.

private int maxLevel = 0;

private void leftView(Node node) {
    printLeft(node, 1);
}

private void printLeft(Node node, int level) {
    if (node == null) {
        return;
    }

    if (maxLevel < level) {
        System.out.print(node.key + " ");
        maxLevel = level;
    }

    printLeft(node.left, level + 1);
    printLeft(node.right, level + 1);
}

Time complexity: O(n), Auxilary Space: O(h)

Similar Problem: 199. Binary Tree Right Side View

8. Children Sum Property

Check whether the given tree follows the children’s sum property or not. Children’s sum property means the sum of left and right children should be equal to the root. Problem: 2236. Example of such trees:-

      10
     /  \
    8    2

      15
     /  \
   9     6
  / \   / \
 4   5 2   4

An empty tree and a tree having only a root element also satisfy these conditions.
Tree = null, Output: true
Tree = 5, Output: true

public class BinaryTree {
    Node root;

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(20);
        tree.root.left = new Node(8);
        tree.root.right = new Node(12);
        tree.root.left.left = new Node(3);
        tree.root.left.right = new Node(5);

        System.out.println(tree.isChildrenSum(tree.root));
    }

    private boolean isChildrenSum(Node node) {
        if (node == null || (node.left == null && node.right == null)) {
            return true;
        }

        int leftValue = (node.left != null ? node.left.key : 0);
        int rightValue = (node.right != null ? node.right.key : 0);

        return node.key == leftValue + rightValue 
                && isChildrenSum(node.left) 
                && isChildrenSum(node.right);
    }
}

Time complexity: O(n), Auxiliary Space: O(h)

9. Check for Balanced Tree

Check whether the tree is height-balanced or not. Height balance means the difference between the height of the left subtree and right subtree should not be more than 1. It should be true for every subtree.

Examples of Balanced Tree:-

Examples of Unbalanced Tree:-

       3
     /   \
    4     8
   / \     \
  5   9     7
           /
          6
// At node.key = 8, 
// left sub tree height = 0
// right sub tree height = 2

Tree Structure:-

public class BinaryTree {
    Node root;

    private void createTree() {
        root = new Node(30);
        root.left = new Node(40);
        root.right = new Node(80);
        root.left.left = new Node(50);
        root.left.right = new Node(70);
        root.right.left = new Node(5);
        root.left.right.left = new Node(20);
        root.left.right.right = new Node(10);
    }

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.createTree();
        System.out.println(tree.isBalanced(tree.root));
    }

    private boolean isBalanced(Node node) {
        // TODO
    }
}

Naive Solution (O^2):- Find the height of the left subtree, and right subtree, and compare their heights.

private boolean isBalanced(Node node) {
    if (node == null) {
        return true;
    }
    int lh = height(node.left);
    int rh = height(node.right);
    return Math.abs(lh - rh) <= 1 && 
           isBalanced(node.left) && 
           isBalanced(node.right);
}

private int height(Node node) {
    if (node == null) {
        return 0;
    }
    return 1 + Math.max(height(node.left), height(node.right));
}

Efficient Solution O(n): Every node returns two things- height and isBalance. The trick is to return -1 if the subtree is unbalanced, and height if it is balanced.

private int isBalanced(Node node) {
    if (node == null) {
        return 0;
    }

    int lh = isBalanced(node.left);
    if (lh == -1) {
        return -1;
    }

    int rh = isBalanced(node.right);
    if (rh == -1) {
        return -1;
    }

    return Math.abs(lh - rh) > 1 ? -1 : Math.max(lh, rh) + 1;
}

10. Maximum Width of Binary Tree

      10
     /  \
    20   30
   / \    \
  40  50   60
 /
80
// Output: 3

  10
 /
80
 \
  70
// Output: 1

         8
      /     \
     30      20
    / \      / \
   90 100  70   300
// Output: 4

Input: null, output: 0
Input: 5, output: 1

private int maxWidth(Node node) {
    if (node == null) {
        return 0;
    }

    Queue<Node> q = new LinkedList<>();
    q.add(node);
    int max = 1;

    while (!q.isEmpty()) {
        int count = q.size();
        max = Math.max(max, count);

        for (int i = 0; i < count; i++) {
            Node curr = q.poll();

            if (curr.left != null) {
                q.offer(curr.left);
            }

            if (curr.right != null) {
                q.offer(curr.right);
            }
        }
    }
    return max;
}

Time complexity: O(n), Auxiliary Space: O(width)

11. Convert Binary Tree to Doubly Linked List

Converting a binary tree to a doubly linked list (DLL) is done using an inorder traversal. This means that the nodes will appear in the linked list in the same order as they would in an inorder traversal (left => root => right) of the binary tree. Make it in-place means do not use another memory to represent the doubly linked list.

       10
      /  \
     5   20
         / \
        30  35
// DLL: 5 <-> 10 <-> 30 <-> 20 <-> 35

      5
     / \
    8   19
        /
       6
// DLL: 8 <-> 5 <-> 6 <-> 19

      10
     /
    8
   /
  7
// DLL: 7 <-> 8 <-> 10

public class BinaryTree {
    Node root;

    private void createTree() {
        root = new Node(10);
        root.left = new Node(5);
        root.right = new Node(20);
        root.right.left = new Node(30);
        root.right.right = new Node(35);
    }

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.createTree();
        Node head = tree.bTToDll(tree.root);
        printDll(head);
    }

    private Node bTToDll(Node rt) {
        // TODO
    }

    private static void printDll(Node head) {
        if (head == null) {
            return;
        }
        Node curr = head;
        while (curr != null) {
            System.out.print(curr.key + " ");
            curr = curr.right;
        }
    }
}

class Node {
    Node left;
    int key;
    Node right;

    public Node(int key) {
        this.key = key;
    }
}

We can use the left reference of the tree as the previous reference of the doubly linked list and the right reference of the tree as the next reference of the doubly linked list.

Node prev = null; // instance variable

private Node bTToDll(Node root) {
    if (root == null) {
        return root;
    }

    // left part
    Node head = bTToDll(root.left);

    // process current node
    if (prev == null) {
        head = root;
    } else {
        root.left = prev;
        prev.right = root;
    }
    prev = root;

    // right part
    bTToDll(root.right);

    return head;
}

Time complexity: O(n), Auxiliary Space: O(h)

12. Construct Binary Tree From Inorder and Preorder

We can construct Binary Tree only from Inorder and Preorder combination or Inorder and Postorder combination. We can construct a binary tree from the preorder and postorder combination. For construction of the binary tree, inorder must be given.

in[] = {20, 10, 30}
pre[] = {10, 20, 30}

       10
      /  \
     20  30

in[] = {40, 20, 50, 10, 30, 80, 70, 90}
pre[] = {10, 20, 40, 50, 30, 70, 80, 90}

             10
           /    \
         20      30
        /  \       \
      40   50     70
                   /  \
                 80   90

Inorder: left => root => right
Preorder = root => left => right

We will construct the tree in preorder faction. We will maintain preindex variable and will construct the node by increasing preindex variable.

public class BinaryTree {

    public static void main(String[] args) {
        int in[] = { 40, 20, 50, 10, 30, 80, 70, 90 };
        int pre[] = { 10, 20, 40, 50, 30, 70, 80, 90 };
        BinaryTree tree = new BinaryTree();
        Node root = tree.cTree(in, pre, 0, in.length - 1);

        // Optional: print the inorder traversal to verify
        tree.printInorder(root);
    }

    int preIndex = 0; // Keeps track of the current index in preorder array

    /**
     * Constructs the binary tree from inorder and preorder traversal arrays.
     * 
     * @param in     Inorder traversal array
     * @param pre    Preorder traversal array
     * @param iStart Starting index of the current subtree in inorder array
     * @param iEnd   Ending index of the current subtree in inorder array
     * @return The root node of the constructed binary tree
     */
    private Node cTree(int[] in, int[] pre, int iStart, int iEnd) {
        // Base case: if there are no elements to construct the subtree
        if (iStart > iEnd) {
            return null;
        }

        // Pick current node from preorder traversal using preIndex and increment preIndex
        Node root = new Node(pre[preIndex++]);

        // Find the index of this node in inorder traversal array
        int inIndex = findIndex(in, iStart, iEnd, root.key);

        // Recursively build the left and right subtrees
        root.left = cTree(in, pre, iStart, inIndex - 1); // Left subtree
        root.right = cTree(in, pre, inIndex + 1, iEnd);  // Right subtree

        return root;
    }

    /**
     * Utility method to find the index of a given value in an array within a specified range.
     * 
     * @param arr    The array to search in
     * @param start  The starting index of the range
     * @param end    The ending index of the range
     * @param value  The value to find
     * @return The index of the value in the array
     */
    private int findIndex(int[] arr, int start, int end, int value) {
        for (int i = start; i <= end; i++) {
            if (arr[i] == value) {
                return i;
            }
        }
        return -1; // This should never happen if input arrays are valid
    }

    // Optional: method to print inorder traversal
    private void printInorder(Node node) {
        if (node == null) {
            return;
        }
        printInorder(node.left);
        System.out.print(node.key + " ");
        printInorder(node.right);
    }
}

class Node {
    Node left;
    int key;
    Node right;

    public Node(int key) {
        this.key = key;
    }
}

Time Complexity: O(n^2) in the worst case. Auxiliary Space: O(n) due to the recursion stack.

To improve the time complexity of constructing a binary tree from inorder and preorder traversals, we can use a hash map (or hash table) to store the indices of elements in the inorder array. This allows us to quickly look up the index of any element in constant time, reducing the overall time complexity to O(n).

Here’s how we can do it:

Preprocess the Inorder Array: Create a hash map to store the index of each element in the inorder array.
Modify the Construction Function: Use the hash map to find the index of the current root in constant time.

import java.util.HashMap;
import java.util.Map;

public class BinaryTree {

    private int preIndex = 0; // Keeps track of the current index in preorder array

    public static void main(String[] args) {
        int in[] = { 40, 20, 50, 10, 30, 80, 70, 90 };
        int pre[] = { 10, 20, 40, 50, 30, 70, 80, 90 };

        BinaryTree tree = new BinaryTree();
        Node root = tree.buildTree(in, pre);

        // Optional: print the inorder traversal to verify
        tree.printInorder(root);
    }

    public Node buildTree(int[] in, int[] pre) {
        Map<Integer, Integer> inMap = new HashMap<>();
        for (int i = 0; i < in.length; i++) {
            inMap.put(in[i], i);
        }
        return constructTree(in, pre, 0, in.length - 1, inMap);
    }

    private Node constructTree(int[] in, int[] pre, int inStart, int inEnd, Map<Integer, Integer> inMap) {
        if (inStart > inEnd) {
            return null;
        }

        // Pick current node from preorder traversal using preIndex and increment preIndex
        Node root = new Node(pre[preIndex++]);

        // Find the index of this node in inorder traversal using the map
        int inIndex = inMap.get(root.key);

        // Recursively build the left and right subtrees
        root.left = constructTree(in, pre, inStart, inIndex - 1, inMap); // Left subtree
        root.right = constructTree(in, pre, inIndex + 1, inEnd, inMap);  // Right subtree

        return root;
    }

    // Optional: method to print inorder traversal
    private void printInorder(Node node) {
        if (node == null) {
            return;
        }
        printInorder(node.left);
        System.out.print(node.key + " ");
        printInorder(node.right);
    }
}

class Node {
    Node left;
    int key;
    Node right;

    public Node(int key) {
        this.key = key;
    }
}

Time Complexity: O(n) in the worst case. Auxiliary Space: O(n) due to the recursion stack.

13. Tree Traversal in Spiral Form

Given the root of a binary tree, return the zigzag level order traversal of its nodes’ values. (i.e., from left to right, then right to left for the next level and alternate between). Problem: 103

Root => Level-1 Right to left => Level-2 Left to Right => Level-3 right to left => Level-4 left to right => and so on.

       1
     /   \
   2      3
 /  \   /  \
4   5  6   7
/ \    /
8  9  10

O/P: 1 3 2 4 5 6 7 10 9 8

        10
       /  \
     20    30
           /  \
         40   50
        /  \    \
      60   70   80

O/P: 10 30 20 40 50 80 70 60

Tree Structure:-

public class BinaryTree {
    Node root;

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.buildTree();
        tree.printSpiral(tree.root);
        // 1 3 2 4 5 6 7 10 9 8 
    }

    private void printSpiral(Node node) {
        // TODO
    }

    private void buildTree() {
        root = createNode(1);
        root.left = createNode(2);
        root.right = createNode(3);
        root.left.left = createNode(4);
        root.left.right = createNode(5);
        root.left.left.left = createNode(8);
        root.left.left.right = createNode(9);
        root.right.left = createNode(6);
        root.right.right = createNode(7);
        root.right.left.left = createNode(10);
    }

    private Node createNode(int key) {
        return new Node(key);
    }
}

class Node {
    Node left;
    int key;
    Node right;

    public Node(int key) {
        this.key = key;
    }
}

Method-1: Using Queue and Stack

It is based on line-by-line level order traversal. We will take a Boolean variable “reverse” initialized as false, and we will make it reverse = !reverse in each iteration. In each iteration, if the reverse is true then put elements from the queue to stack (to display in reverse order) else directly display the element.

private void printSpiral(Node node) {
    if (node == null) {
        return;
    }

    Queue<Node> q = new LinkedList<>();
    q.offer(node);

    Stack<Node> s = new Stack<>();
    boolean reverse = false;

    while (!q.isEmpty()) {
        int count = q.size();
        for (int i = 0; i < count; i++) {
            Node curr = q.poll();
            if (reverse) {
                s.push(curr);
            } else {
                System.out.print(curr.key + " ");
            }
            if (curr.left != null) {
                q.offer(curr.left);
            }
            if (curr.right != null) {
                q.offer(curr.right);
            }
        }
        if (reverse) {
            int stackSize = s.size();
            for (int i = 0; i < stackSize; i++) {
                System.out.print(s.pop().key + " ");
            }
        }
        reverse = !reverse;
    }
}

Time Complexity: O(n), Auxiliary Space: O(n)

Can we optimize it through any data structure so that every node can enter and exit the data structure exactly once? In this solution some elements are processed twice:- once in the queue and again in the stack.

Method-2: Using 2 Stack

We can use 2 stacks. The first level goes into stack 1 and the second level goes into stack 2. We will poll items from stack 1 and push its child items into stack 2. Similarly, we will poll items from stack 2 and push their child items into stack 1 in reverse order. Steps:-

Push root to the stack s1.
While neither of the two stacks is empty:-
- While s1 is not empty.
  - Take out a node, and print it.
  - Push children of the taken-out node into s2.
- While s2 is not empty.
  - Take out a node, and print it.
  - Push children of the taken-out node into s1 in reverse order (first push the right child then the left child).

private void printSpiral(Node node) {
    if (node == null) {
        return;
    }

    Stack<Node> s1 = new Stack<>();
    s1.add(node);
    Stack<Node> s2 = new Stack<>();

    while (!s1.isEmpty() || !s2.isEmpty()) {
        int size1 = s1.size();
        int size2 = s2.size();

        if (size1 != 0) {
            // process stack s1
            for (int i = 0; i < size1; i++) {
                Node curr = s1.pop();
                System.out.print(curr.key + " ");

                if (curr.left != null) {
                    s2.push(curr.left);
                }
                if (curr.right != null) {
                    s2.push(curr.right);
                }
            }
        } else {
            // process stack s2
            for (int i = 0; i < size2; i++) {
                Node curr = s2.pop();
                System.out.print(curr.key + " ");

                // first put right child
                if (curr.right != null) {
                    s1.push(curr.right);
                }
                // then put left child
                if (curr.left != null) {
                    s1.push(curr.left);
                }
            }
        }
    }
}

In this approach, we are not processing any item twice. Time Complexity: O(n), Auxiliary Space: O(n).

14. Diameter of a Binary Tree

The diameter of a binary tree is the length of the longest path between any two nodes in the tree. This path may or may not pass through the root. Problem Link: 153

        1
       / \
      2   3
     / \   \
    4   5   6
   /         \
  7           8

In this example, the diameter is the length of the longest path between any two nodes. The longest path goes through nodes 7, 4, 2, 1, 3, 6, and 8. The diameter would be 6 edges.

Output: 5 (20, 10, 30, 40, 60)

Input: null
Output: 0

Input: 10
Output: 1

        10
       /  \
     20    60
    /  \
   30   80
  / \    \
 40  50   90
 /         \
60          18

Output: 7 (60, 40, 30, 20, 80, 90, 18)

public class BinaryTree {
    Node root;

    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree();
        tree.root = new Node(10);
        tree.root.left = new Node(20);
        tree.root.right = new Node(60);
        tree.root.left.left = new Node(30);
        tree.root.left.right = new Node(80);
        tree.root.left.left.left = new Node(40);
        tree.root.left.left.right = new Node(50);
        tree.root.left.left.left.left = new Node(60);
        tree.root.left.right.right = new Node(90);
        tree.root.left.right.right.right = new Node(18);

        System.out.println(tree.diameter(tree.root));
    }

    private int diameter(Node node) {
        // TODO
    }
}

class Node {
    Node left;
    int key;
    Node right;

    public Node(int key) {
        this.key = key;
    }
}

Idea: Find the following value for every node and return the maximum:- max(1 + lh + rh) where lh is left height, rh is right height.

Naive Solution: O(n^2)

private int diameter(Node node) {
    if (node == null) {
        return 0;
    }

    int d1 = 1 + height(node.left) + height(node.right);
    int d2 = diameter(node.left);
    int d3 = diameter(node.right);

    return Math.max(d1, Math.max(d2, d3));
}

private int height(Node node) {
    if (node == null) {
        return 0;
    }

    return 1 + Math.max(height(node.left), height(node.right));
}

Better O(n): Precompute the height of every node and store it in a map, then we can get the height in O(1) time. Therefore the time complexity will be O(n) time and Auxiliary space O(n).

Efficient Solution O(n) without Overhead of Map
The height() function returns height but sets the res variable to have diameter.

int res = 0;

private int height(Node node) {
    if (node == null) {
        return 0;
    }

    int lh = height(node.left);
    int rh = height(node.right);

    // calculate diameter
    res = Math.max(res, 1 + rh + lh);

    return 1 + Math.max(lh, rh);
}

private int diameter(Node node) {
    height(node);
    return res;
}

Time complexity: O(n), Auxiliary Space: O(h) from recursion stack.

15. Lowest Common Ancestor (LCA) of Binary Tree

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree. The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself). Problem: 236

        10
       /  \
     20    30
          /  \
         40   50
        /     / \
       60    70 80

n1 = 60
n2 = 70
O/P: 30

More examples in the same tree:
LCA(20, 80) = 10
LCA(80, 30) = 30
LCA(70, 80) = 50

It is also useful to find the distance between two nodes.

class TreeNode {
    int val;
    TreeNode left, right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class BinaryTree {
    public static void main(String[] args) {
        TreeNode root = new TreeNode(10);

        root.left = new TreeNode(50);
        root.right = new TreeNode(60);

        root.left.left = new TreeNode(70);
        root.left.right = new TreeNode(20);

        root.left.left.left = new TreeNode(40);

        root.left.right.left = new TreeNode(90);
        root.left.right.right = new TreeNode(80);

        root.left.right.left.left = new TreeNode(30);

        TreeNode lca = lca(root, 30, 80);
        System.out.println(lca.val);
    }

    private static TreeNode lca(TreeNode root, int n1, int n2) {
        // TODO
    }
}

Naive Solution

Build two path arrays. Path1 array has nodes from root to node1, and Path2 array has nodes from root to node2.

n1 = 30, n2 = 80
path1[ ] = {10, 50, 20, 90, 30}
path2[ ] = {10, 50, 20, 80}
LCA = 20

private static TreeNode lca(TreeNode root, int n1, int n2) {
    ArrayList<TreeNode> path1 = new ArrayList<>();
    ArrayList<TreeNode> path2 = new ArrayList<>();

    if (!findPath(root, path1, n1) || !findPath(root, path2, n2)) {
        return null;
    }

    for (int i = 0; i < path1.size() - 1 && i < path2.size() - 1; i++) {
        if (path1.get(i + 1) != path2.get(i + 1)) {
            return path1.get(i);
        }
    }

    return null;
}

private static boolean findPath(TreeNode root, ArrayList<TreeNode> path, int n) {
    if (root == null) {
        return false;
    }

    path.add(root);

    if (root.val == n) {
        return true;
    }

    if (findPath(root.left, path, n) || findPath(root.right, path, n)) {
        return true;
    }

    path.remove(path.size() - 1);
    return false;
}

Time Complexity:- Θ(n) for findPath for path1 + Θ(n) for findPath for path2 + O(n) traversing of list = Θ(n). Auxiliary space: O(n).

Efficient Solution

Requires one traversal and Θ(h) extra space for the recursive traversal.
Assumes that both n1 and n2 exist in the tree. It does not give correct result when only one (n1 or n2) exists.

Idea: We do normal recursive traversal. We have the following cases for every node.

If it is same as n1 or n2, return the node.
If one of its subtrees contain n1 and other contains n2.
If one of its subtrees contain both n1 and n2.
If none of its subtrees contain any of n1 and n2.

private static TreeNode lca(TreeNode root, int n1, int n2) {
    if (root == null) {
        return null;
    }

    if (root.val == n1 || root.val == n2) {
        return root;
    }

    TreeNode lca1 = lca(root.left, n1, n2);
    TreeNode lca2 = lca(root.right, n1, n2);

    if (lca1 != null && lca2 != null) {
        return root;
    }

    if (lca1 != null) {
        return lca1;
    }

    return lca2;
}

Time Complexity:- O(n); Auxiliary space: Θ(n)

16. Burn a Binary Tree From a Leaf

Given a binary tree and a leaf node from which a fire starts, determine the time (in terms of edges traversed) it takes to burn the entire tree. The fire spreads to adjacent nodes (parent, left child, right child) every second.

Constraints:

The tree is a binary tree.
The fire starts from a given leaf node.
The time to burn an edge is 1 second.

    10
   /  \
  20   30
 /  \    \
40  50   60

Leaf = 50
Output: 4

Explanation: The following nodes are burned during:

Minute 0: Node 50
Minute 1: Nodes 20
Minute 2: Node 40 and 10
Minute 3: Node 30
Minute 4: Nodes 60
It takes 4 minutes for the whole tree to be burned so we return 4.

leaf = 50
Output: 3

    10
   /
  20

leaf = 50
Output: -1

Leaf = 50
Output: 4

In this problem, we actually have to find out the farthest node from the given leaf.
The farthest node must be reachable through one of the ancestors (50, 30, 20, and 10)

Distance through 50 = 0
Distance through 30 = 4
Distance through 20 = 3
Distance through 10 = 3

We will take idea from the problem diameter of the tree.

The burnTree() method does 2 things:-

Return Height
Set distance if the given leaf is a descendent.

class TreeNode {
    int val;
    TreeNode left, right;

    TreeNode(int val) {
        this.val = val;
        this.left = this.right = null;
    }
}

class Distance {
    // initially the distance.val should be -1
    int val;

    Distance(int d) {
        val = d;
    }
}

public class BinaryTree {
    // res is shared by all recursive function call
    private int res = 0;

    private int burnTree(TreeNode root, int leaf, Distance dist) {
        if (root == null) {
            return 0;
        }
        if (root.val == leaf) {
            dist.val = 0;
            return 1;
        }
        Distance ldist = new Distance(-1);
        Distance rdist = new Distance(-1);

        int lh = burnTree(root.left, leaf, ldist);
        int rh = burnTree(root.right, leaf, rdist);

        if (ldist.val != -1) {
            dist.val = ldist.val + 1;
            res = Math.max(res, rh + dist.val);
        } else if (rdist.val != -1) {
            dist.val = rdist.val + 1;
            res = Math.max(res, lh + dist.val);
        }
        return Math.max(lh, rh) + 1;
    }

    private int burnTreeFromLeaf(TreeNode root, int leaf) {
        Distance distance = new Distance(-1);
        burnTree(root, leaf, distance);
        return res; 
    }

    public static void main(String[] args) {
        TreeNode root = new TreeNode(10);

        root.right = new TreeNode(20);

        root.right.left = new TreeNode(5);
        root.right.right = new TreeNode(30);

        root.right.right.left = new TreeNode(50);
        root.right.right.right = new TreeNode(40);

        root.right.right.right.right = new TreeNode(60);

        root.right.right.right.right.right = new TreeNode(70);

        BinaryTree tree = new BinaryTree();
        System.out.println(tree.burnTreeFromLeaf(root, 50));
    }
}

17. Count Nodes in a Complete Binary Tree

Given a complete binary tree, count the number of nodes present in the tree.

A complete binary tree is a type of binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible. Problem: 222

Input: root = [1,2,3,4,5,6] Output: 6

    1
   /  \
  2    3
 / \   / \
4  5   6  7

Input: root = [1,2,3,4,5,6,7] Output: 7

class TreeNode {
    int val;
    TreeNode left, right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class BinaryTree {
    public static void main(String[] args) {
        TreeNode root = new TreeNode(1);

        // Level 1
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);

        // Level 2
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);
        root.right.left = new TreeNode(6);
        root.right.right = new TreeNode(7);

        BinaryTree tree = new BinaryTree();
        System.out.println(tree.countNode(root));
    }

    private int countNode(TreeNode root) {
        // TODO
    }
}

Naive Solution O(n)

private int countNode(TreeNode root) {
    if (root == null) {
        return 0;
    }
    return 1 + countNode(root.left) + countNode(root.right);
}

This solution works for every binary tree whether it is a complete Binary Tree or not. Time complexity Θ(n) and Auxiliary space O(n).

Efficient Solution O(log n * log n)

private int countNode(TreeNode root) {
    int lh = 0, rh = 0;

    // Calculate height of leftmost node
    for (TreeNode curr = root; curr != null; curr = curr.left) {
        lh++;
    }

    // Calculate height of rightmost node
    for (TreeNode curr = root; curr != null; curr = curr.right) {
        rh++;
    }

    if (lh == rh) {
        // The tree is a perfect binary tree
        return (int) (Math.pow(2, rh) - 1);
    }

    // Recursively count nodes in left and right subtrees
    // same as naive solution
    return 1 + countNode(root.left) + countNode(root.right);
}

In the worst case, the overall time complexity is 𝑂((log⁡ 𝑛)^2) for a complete binary tree, as the height h of a complete binary tree is log 𝑛.

18. Serialize and Deserialize a Binary Tree

Serialization is the process of converting a binary tree into a format that can be easily stored or transmitted, and deserialization is the process of converting this format back into the original binary tree structure. Problem: 297 Hard. Solution.

Requirements:

Serialize: Implement a method to serialize a binary tree into a string.
Deserialize: Implement a method to deserialize the string back into the original binary tree.

Serialized Output: [1, 2, 3, null, null, 4, 5]

Serialization Steps

Initialize:
- Use an empty string for the serialized output.
- Use a Queue for level-order traversal.
Process Nodes:
- Add the root to the queue.
- While the queue is not empty:
  - Dequeue a node.
  - Add its value to the string (use null for missing nodes).
  - Enqueue its children.

Deserialization Steps

Initialize:
- Use a Queue for level-order construction.
- Split the serialized string by commas to get node values.
Start with the Root:
- Create the root node from the first value.
- Add the root to the queue.
Process Nodes:
- While the queue is not empty, do the following for each node:
  - Dequeue a node.
  - Use the next values for its left and right children.
  - If a value is not null, create the child node and enqueue it.
  - If a value is null, set the child reference to null.

import java.util.*;

class TreeNode {
    int val;
    TreeNode left, right;

    TreeNode(int val) {
        this.val = val;
    }
}

public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        // If the root is null, return an empty string.
        if (root == null) {
            return "";
        }

        // Use a queue to perform level-order traversal (BFS).
        Queue<TreeNode> q = new LinkedList<>();
        q.offer(root);
        StringBuilder sb = new StringBuilder();

        while (!q.isEmpty()) {
            // Process nodes level by level.
            TreeNode node = q.poll();
            if (node == null) {
                sb.append("n "); // Append "n" for null nodes.
            } else {
                sb.append(node.val).append(" "); // Append node value.
                q.offer(node.left); // Add left child to the queue.
                q.offer(node.right); // Add right child to the queue.
            }
        }
        return sb.toString().trim(); // Remove trailing space.
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        // If the data is empty or null, return null.
        if (data.isBlank()) {
            return null;
        }

        // Split the data string into an array of values.
        String[] values = data.split(" ");
        // Create the root node with the first value.
        TreeNode root = new TreeNode(Integer.parseInt(values[0]));
        // Use a queue to help construct the tree.
        Queue<TreeNode> q = new LinkedList<>();
        q.add(root);
        int i = 1; // Index for iterating over the values array.

        while (!q.isEmpty()) {
            // Get the current node from the queue.
            TreeNode parent = q.poll();

            // Check if there is a left child.
            if (!values[i].equals("n")) {
                TreeNode left = new TreeNode(Integer.parseInt(values[i]));
                parent.left = left; // Assign left child to parent.
                q.offer(left); // Add left child to the queue.
            }
            i++;

            // Check if there is a right child.
            if (i < values.length && !values[i].equals("n")) {
                TreeNode right = new TreeNode(Integer.parseInt(values[i]));
                parent.right = right; // Assign right child to parent.
                q.offer(right); // Add right child to the queue.
            }
            i++;
        }

        return root;
    }

    public static void main(String[] args) {
        Codec codec = new Codec();

        // Example tree
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.right.left = new TreeNode(4);
        root.right.right = new TreeNode(5);

        // Serialize the tree
        String serialized = codec.serialize(root);
        System.out.println("Serialized Output: " + serialized);

        // Deserialize the string back to tree
        TreeNode deserializedRoot = codec.deserialize(serialized);
        System.out.println("Deserialized Root Value: " + deserializedRoot.val);

        // Additional test to verify the entire tree
        System.out.println(codec.serialize(deserializedRoot)); // Should match the original serialization
    }
}

19. Iterative Inorder and Preorder Traversal

Inorder Traversal => left, root, right
Preorder Traversal => root, left, right

public class BinaryTree {
    TreeNode root;

    public static void main(String[] args) {
        BinaryTree bt = new BinaryTree();
        bt.root = new TreeNode(10);
        bt.root.left = new TreeNode(20);
        bt.root.right = new TreeNode(30);
        bt.root.right.left = new TreeNode(40);
        bt.root.right.right = new TreeNode(50);

        // bt.preorder(bt.root);
        System.out.println();

        // bt.inorder(bt.root);
        System.out.println();
    }
}

class TreeNode {
    TreeNode left;
    int key;
    TreeNode right;

    public TreeNode(int key) {
        this.key = key;
    }
}

Iterative Inorder Traversal

To perform an iterative inorder traversal of a binary tree, you can use a stack to simulate the recursive call stack used in a traditional inorder traversal. Here’s how you can implement it in your BinaryTree class:

Stack Initialization: Use a stack to keep track of nodes.
Traversal:
- Push the current node and all its left descendants to the stack.
- When you reach a node with no left child, pop from the stack, process the node (print its key), and move to its right subtree.
While Loop: Continue this process until all nodes are processed (i.e., until both the stack is empty and the current node is null).

This approach ensures that the inorder traversal is performed iteratively, correctly visiting nodes in the left-root-right order without using recursion.

private void inorder(TreeNode node) {
    if (node == null) {
        return;
    }

    Stack<TreeNode> stack = new Stack<>();
    TreeNode curr = node;

    while (curr != null || !stack.isEmpty()) {
        // Reach the leftmost node of the current node
        while (curr != null) {
            stack.push(curr);
            curr = curr.left;
        }

        // Current must be null at this point
        curr = stack.pop();
        System.out.print(curr.key + " ");

        // Visit the right subtree
        curr = curr.right;
    }
}

This program push each node to the stack exactly once and pop each node exactly once therefore the time complexity is Θ(n). Axillary space: O(h) where h is the height of the binary tree.

Iterative Preorder Traversal

To perform an iterative preorder traversal of a binary tree, you can use a stack to simulate the recursive call stack used in a traditional preorder traversal. Here’s a step-by-step approach to achieving this:

Steps for Iterative Preorder Traversal:-

Initialize the Stack:
- Create a stack and push the root node onto the stack.
Traverse the Tree:
- While the stack is not empty:
  - Pop the node from the top of the stack.
  - Process the node (print its key or store its value).
  - Push the right child of the node onto the stack (if it exists).
  - Push the left child of the node onto the stack (if it exists).

Key Points:

In preorder traversal, the order is: Root, Left, Right.
By pushing the right child first, you ensure that the left child is processed first because of the stack’s LIFO (Last In, First Out) property.

We can notice that it is very similar to level order traversal. In level order traversal we were using Queue and pushing left element first but here we are using Stack and pushing right element first.

private void preorder(TreeNode node) {
    if (node == null) {
        return;
    }

    Stack<TreeNode> s = new Stack<>();
    s.push(node);

    while (!s.isEmpty()) {
        TreeNode curr = s.pop();
        System.out.print(curr.key + " ");

        // Push right child first so that left is processed first
        if (curr.right != null) {
            s.push(curr.right);
        }
        if (curr.left != null) {
            s.push(curr.left);
        }
    }
}

Time Complexity ( O( n ) ): Each node is pushed and popped from the stack once, resulting in a linear time complexity relative to the number of nodes.
Space Complexity ( O( n ) ): The stack space depends on the height of the tree. In the worst-case scenario, this can be ( O( n ) ) if the tree is completely unbalanced. In the best-case scenario for a balanced tree, this would be ( O( log n ) ).

Space Optimized Solution

It will have the same time complexity O(n) but auxiliary space O(h).

Initialize the Stack:
- Create a stack and push the root node onto the stack.
- Current as root
Traverse the Tree:
- While the stack is not empty:
  - While the current is not null
    - Process the node (print its key or store its value).
    - Push the right child of the node onto the stack (if it exists).
    - Make current = current.left
  - Pop the node from the top of the stack and assign it to the current.

private void preorder(TreeNode node) {
    if (node == null) {
        return;
    }

    Stack<TreeNode> s = new Stack<>();
    s.push(node);
    TreeNode curr = node;

    while (!s.isEmpty()) {
        while (curr != null) {
            System.out.print(curr.key + " ");
            if (curr.right != null) {
                s.push(curr.right);
            }
            curr = curr.left;
        }
        curr = s.pop();
    }
}

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!

Binary Tree

Tree Traversal

1. Height of Binary Tree

2. Print Nodes at Distance K

3. Level Order Traversal or Breadth First Search (BFS)

4. Level Order Traversal Line by Line

5. Size of a Binary Tree

6. Maximum in Binary Tree

7. Print Left View of Binary Tree

8. Children Sum Property

9. Check for Balanced Tree

10. Maximum Width of Binary Tree

11. Convert Binary Tree to Doubly Linked List

12. Construct Binary Tree From Inorder and Preorder

13. Tree Traversal in Spiral Form

14. Diameter of a Binary Tree

15. Lowest Common Ancestor (LCA) of Binary Tree

16. Burn a Binary Tree From a Leaf

17. Count Nodes in a Complete Binary Tree

18. Serialize and Deserialize a Binary Tree

19. Iterative Inorder and Preorder Traversal

Iterative Inorder Traversal

Iterative Preorder Traversal

Leave a Comment Cancel Reply