Matrix Multiplication in Java

In this post, we will discuss Matrix Multiplication in Java | How to find Multiplication of two matrix in java? How to write a Java program to multiply two matrices? What are the different techniques to find the matrix multiplication in Java? Since a matrix is also known as an array of arrays, therefore matrix multiplication can be called array multiplication in Java.

What is Matrix Multiplication?

Let A be an m×k matrix and B be a k ×n matrix. The product of A and B, denoted by AB, is the m × n matrix with its (i, j )th entry equal to the sum of the products of the corresponding elements from the ith row of A and the jth column of B. In other words, if AB =[c_ij], then c_ij = a_i1b_1j + a_i2b_2j +···+a_ikb_kj.

Condition for the Matrix multiplication:- The product of two matrices is not defined when the number of columns in the first matrix and the number of rows in the second matrix are not the same.

Example of Matrix Multiplication,

The product of A and B is denoted as AB and it can be calculated as AB=
(a11*b11+a12*b21) (a11*b12+a12*b22)
(a21*b11+a22*b21) (a21*b12+a22*b22)

Example using 2×2 matrices,

A = 
1 3
7 5

B = 
6 8
4 2

C = 
1*6+3*4  1*8+3*2
7*6+5*4  7*8+5*2

=
18 14
62 66

Java Method to find Matrix Multiplication for Square Matrix

// method to calculate product of two matrix
public static int[][] multiplyMatrix(int[][] a, int[][] b) {

   // find size of matrix
   // (Assuming both matrix is square matrix
   // of same size)
   int size = a.length;

   // declare new matrix to store result
   int product[][] = new int[size][size];

   // find product of both matrices
   // outer loop 
   for (int i = 0; i < size; i++) {
     // inner-1 loop 
     for (int j = 0; j < size; j++) {
       // assign 0 to the current element
       product[i][j] = 0;

       // inner-2 loop 
       for (int k = 0; k < size; k++) {
         product[i][j] += a[i][k] * b[k][j];
       }
     }
   }

   return product;
}

Time Complexity:- O(N³)

Why does it need three for loops? For accessing all the elements of any matrix we need two for loop. But for finding the product requires one additional for loop. Therefore the time complexity is O(N³).

Matrix Multiplication in Java Using Methods

In this program, values for the matrices are already given just call the method to multiply both matrices, and then display the resultant matrix.

import java.util.Arrays;

public class Matrix {

  // main method
  public static void main(String[] args) {

    // declare and initialize a matrix
    int a[][] = { { 1, 3 }, { 7, 5 } };
    int b[][] = { { 6, 8 }, { 4, 2 } };

    // find size of matrix
    // (Assuming both matrix is square matrix
    // of same size)
    int size = a.length; // 2

    // declare new matrix to store result (2x2)
    int c[][] = new int[size][size];

    // multiplication of matrix
    c = multiplyMatrix(a, b);

    // display all matrices
    System.out.println("A = " + Arrays.deepToString(a));
    System.out.println("B = " + Arrays.deepToString(b));
    System.out.println("C (Product) = " + Arrays.deepToString(c));
  }

  // method to calculate product of two matrix
  public static int[][] multiplyMatrix(int[][] a, int[][] b) {

    // find size of matrix
    // (Assuming both matrix is square matrix
    // of same size)
    int size = a.length;

    // declare new matrix to store result
    int product[][] = new int[size][size];

    // find product of both matrices
    // outer loop 
    for (int i = 0; i < size; i++) {
      // inner-1 loop 
      for (int j = 0; j < size; j++) {
        // assign 0 to the current element
        product[i][j] = 0;

        // inner-2 loop 
        for (int k = 0; k < size; k++) {
          product[i][j] += a[i][k] * b[k][j];
        }
      }
    }

    return product;
  }

}

Output:-

A = [[1, 3], [7, 5]]
B = [[6, 8], [4, 2]]
C (Product) = [[18, 14], [62, 66]]

In this program, to display the matrix we had used deepToString() method of the Arrays class, but you can also use the nested loops. See:- Different ways to print array in Java

Matrix Multiplication by taking Input from the User

In the above program both matrices A and B were initialized within the program, now let us see another Java program for matrix multiplication by taking input values from users using Scanner. If you want then you can also use BufferedReader class.

import java.util.Scanner;

public class Matrix {

  // create Scanner class object to read input
  private static Scanner scan = new Scanner(System.in);

  // main method
  public static void main(String[] args) {

    // declare variables
    int size = 0;
    int a[][] = null; // first matrix
    int b[][] = null; // second matrix
    int c[][] = null; // resultant matrix

    // ask size
    // (assume matrices are square matrix with same size)
    System.out.println("Enter the Size of Matrix,");
    System.out.println("Enter 2 for 2x2, 3 for 3x3 and e.t.c: ");
    size = scan.nextInt();

    // initialize matrices
    a = new int[size][size];
    b = new int[size][size];
    c = new int[size][size];

    // read matrix A and B
    System.out.println("Enter Matrix A: ");
    a = readMatrix(a);
    System.out.println("Enter Matrix B: ");
    b = readMatrix(b);

    // multiplication of matrix
    c = multiplyMatrix(a, b);

    // display resultant matrix
    System.out.println("Result Matrix: "); 
    for(int i=0; i<c.length; i++) {
      for(int j=0; j<c[i].length; j++) {
        System.out.print(c[i][j]+" ");
      }
      System.out.println(); // new line
    }
  }

  // method to read matrix elements as input
  public static int[][] readMatrix(int[][] temp) {
    for (int i = 0; i < temp.length; i++) {
      for (int j = 0; j < temp[0].length; j++) {
        // read matrix elements
        temp[i][j] = scan.nextInt();
      }
    }
    return temp;
  }

  // method to calculate product of two matrix
  public static int[][] multiplyMatrix(int[][] a, int[][] b) {

    // find size of matrix
    // (Assuming both matrix is square matrix
    // of same size)
    int size = a.length;

    // declare new matrix to store result
    int product[][] = new int[size][size];

    // find product of both matrices
    // outer loop
    for (int i = 0; i < size; i++) {
      // inner-1 loop
      for (int j = 0; j < size; j++) {
        // assign 0 to the current element
        product[i][j] = 0;

        // inner-2 loop
        for (int k = 0; k < size; k++) {
          product[i][j] += a[i][k] * b[k][j];
        }
      }
    }

    return product;
  }

}

Output:-

Enter the Size of Matrix,
Enter 2 for 2×2, 3 for 3×3 and e.t.c:
3
Enter Matrix A:
1 2 3
4 5 6
7 8 9
Enter Matrix B:
5 6 7
8 9 10
3 1 2
Result Matrix:
30 27 33
78 75 90
126 123 147

In this program, we had created Scanner class object as a private static variable which is outside of the main method because we need to read input values in two methods, in the main method to read row and column values and in the readMatrix() method to read matrix elements. Therefore instead of creating Scanner class objects in both classes separately, it is better to create them as a static variable only once and use it multiple times anywhere in the program.

Program for Both Square and Non Square matrix

In the above examples we were assuming that matrix is a square matrix, therefore those methods will work only for a square matrix. For non-square matrix, row and column sizes vary. Below Java program is capable to calculate the product of both Square and Non-Square matrices.

public class Matrix {

  // main method
  public static void main(String[] args) {

    // declare and initialize a 3x2 matrix
    int a[][] = { { 1, 2 }, { 3, 4 }, {5, 6} };
    // declare and initialize a 2x4 matrix
    int b[][] = { { 6, 7, 8, 9 }, { 1, 2, 3, 4 } };

    // find row size of first matrix
    int row = a.length; // 3
    // find column size of second matrix
    int column = b[0].length; // 4

    // declare new matrix to store result (3x4)
    int c[][] = new int[row][column];

    // multiplication of matrix
    c = multiplyMatrix(a, b);

    // display all matrices
    System.out.println("Matrix A = ");
    displayMatrix(a);
    System.out.println("Matrix B = ");
    displayMatrix(b);
    System.out.println("Matrix C (Product) = ");
    displayMatrix(c);
  }

  // method to display the matrix
  public static void displayMatrix(int[][] matrix) {
    // outer loop for row
    for(int i=0; i<matrix.length; i++) {
      // inner loop for column
      for(int j=0; j<matrix[i].length; j++) {
        System.out.print(matrix[i][j]+" ");
      }
      System.out.println(); // new line
    }
  }

  // method to calculate product of two matrix
  // matrices can be square or non-square matrix
  public static int[][] multiplyMatrix(int[][] a, int[][] b) {

    // find row size of first matrix
    int row = a.length;
    // find column size of second matrix
    int column = b[0].length;

    // declare new matrix to store result
    int product[][] = new int[row][column];

    // find product of both matrices
    // outer loop upto row of A
    for (int i = 0; i < row; i++) {
      // inner-1 loop utp0 column of B
      for (int j = 0; j < column; j++) {
        // assign 0 to the current element
        product[i][j] = 0;

        // inner-2 loop utpo A[0].length
        for (int k = 0; k < a[0].length; k++) {
          product[i][j] += a[i][k] * b[k][j];
        }
      }
    }

    return product;
  }

}

Output:-

Matrix A =
1 2
3 4
5 6
Matrix B =
6 7 8 9
1 2 3 4
Matrix C (Product) =
8 11 14 17
22 29 36 43
36 47 58 69

Using Divide and Conquer Method

In the divide and conquer method we say that if the problem is larger then we break the problem into sub-problems and solve those sub-problems. Later combine the solutions of sub-problems to get the solution for the actual problem.

If it is a smaller problem then it can be solved directly but if it is a large problem then using divide and conquer break them into small problems. Therefore let us see the solution for the smaller problems.

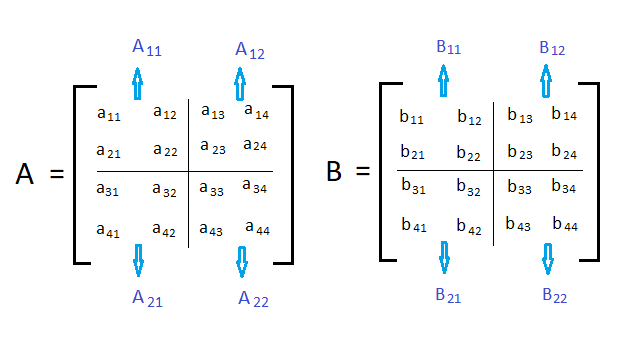
To solve our problem assume 2×2 is the smallest square matrix. Let A and B be two different matrices.

     a11  a12
A = 
     a21  a22

     b11  b12
B = 
     b21  b22

     c11  c12
C = 
     c21  c22

Where C = A*B, The Matrix C can be calculated as,

• c₁₁ = a₁₁*b₁₁ + a₁₂*b₂₁
• c₁₂ = a₁₁*b₁₂ + a₁₂*b₂₂
• c₂₁ = a₂₁*b₁₁ + a₂₂*b₂₁
• c₂₂ = a₂₁*b₁₂ + a₂₂*b₂₂

Since this method requires 8 multiplication and 4 addition therefore it requires constant time. The time complexity is:- O(N³)

What if the size is greater than 2×2? We assume that the matrices are having dimensions in powers of 2 like 2×2, 4×4, 8×8, 16×16, 256×256, and e.t.c. If it is not of power 2×2 then we can fill zeros and makes it a square matrix of 2×2.

See More:- Divide and Conquer Method of Matrix Multiplication

The next matrix multiplication algorithm given by Strassen is also using the divide and conquer technique and gives better performance O(N2.8041) therefore we are not writing the program for this method.

Strassen’s Matrix Multiplication in Java

Strassen’s had given another algorithm for finding the matrix multiplication. Unlike a simple divide and conquer method which uses 8 multiplications and 4 additions, Strassen’s algorithm uses 7 multiplications which reduces the time complexity of the matrix multiplication algorithm a little bit.

The addition and subtraction operation takes less time compared to the multiplication process. In Strassen’s matrix multiplication algorithm, the number of multiplication was reduced but the number of addition and subtraction increased.

See More:- Strassen’s Matrix Multiplication Algorithm

/**
 ** Java Program to Implement Strassen Algorithm
 **/
package com.know.program;
import java.util.Scanner;

public class Matrix {
  
  // create Scanner class object to read input
  private static Scanner scan = new Scanner(System.in);

  // method to calculate product of two matrix
  // Strassen Algorithm
  public int[][] multiply(int[][] a, int[][] b) {

    // find size of matrix
    int n = a.length;

    // create new matrix to store resultant
    int[][] c = new int[n][n];

    /** base case **/
    if (n == 1)
      c[0][0] = a[0][0] * b[0][0];
    else { /* general case */
      int[][] A11 = new int[n / 2][n / 2];
      int[][] A12 = new int[n / 2][n / 2];
      int[][] A21 = new int[n / 2][n / 2];
      int[][] A22 = new int[n / 2][n / 2];
      int[][] B11 = new int[n / 2][n / 2];
      int[][] B12 = new int[n / 2][n / 2];
      int[][] B21 = new int[n / 2][n / 2];
      int[][] B22 = new int[n / 2][n / 2];

      // divide matrix A into 4 halves
      split(a, A11, 0, 0);
      split(a, A12, 0, n / 2);
      split(a, A21, n / 2, 0);
      split(a, A22, n / 2, n / 2);
      // divide matrix B into 4 halves
      split(b, B11, 0, 0);
      split(b, B12, 0, n / 2);
      split(b, B21, n / 2, 0);
      split(b, B22, n / 2, n / 2);
      
      /** 
        * p1 = (A11 + A22)(B11 + B22)
        * p2 = (A21 + A22) B11
        * p3 = A11 (B12 - B22)
        * p4 = A22 (B21 - B11)
        * p5 = (A11 + A12) B22
        * p6 = (A21 - A11) (B11 + B12)
        * p7 = (A12 - A22) (B21 + B22)
        **/

      int[][] p1 = multiply(add(A11, A22), add(B11, B22));
      int[][] p2 = multiply(add(A21, A22), B11);
      int[][] p3 = multiply(A11, sub(B12, B22));
      int[][] p4 = multiply(A22, sub(B21, B11));
      int[][] p5 = multiply(add(A11, A12), B22);
      int[][] p6 = multiply(sub(A21, A11), add(B11, B12));
      int[][] p7 = multiply(sub(A12, A22), add(B21, B22));

      /**
        * C11 = p1 + p4 - p5 + p7
        * C12 = p3 + p5
        * C21 = p2 + p4
        * C22 = p1 - p2 + p3 + p6
        **/

      int[][] C11 = add(sub(add(p1, p4), p5), p7);
      int[][] C12 = add(p3, p5);
      int[][] C21 = add(p2, p4);
      int[][] C22 = add(sub(add(p1, p3), p2), p6);

      /** join 4 halves into one result matrix **/
      join(C11, c, 0, 0);
      join(C12, c, 0, n / 2);
      join(C21, c, n / 2, 0);
      join(C22, c, n / 2, n / 2);
    } // end-of-else-part

    // return resultant matrix
    return c;
  }

  // method to add two matrices
  public int[][] add(int[][] a, int[][] b) {
    int n = a.length;
    int[][] c = new int[n][n];
    for (int i = 0; i < n; i++)
      for (int j = 0; j < n; j++)
        c[i][j] = a[i][j] + b[i][j];
    return c;
  }

  // method to subract two matrices
  public int[][] sub(int[][] a, int[][] b) {
    int n = a.length;
    int[][] c = new int[n][n];
    for (int i = 0; i < n; i++)
      for (int j = 0; j < n; j++)
        c[i][j] = a[i][j] - b[i][j];
    return c;
  }

  // method to split parent matrix into child matrices
  public void split(int[][] parentMatrix, int[][] childMatrix, 
                     int fromIndex, int toIndex) {
    for (int i1=0, i2=fromIndex; i1 < childMatrix.length; i1++, i2++)
      for (int j1=0, j2=toIndex; j1 < childMatrix.length; j1++, j2++)
        childMatrix[i1][j1] = parentMatrix[i2][j2];
  }

  // method to join child matrices into parent matrix
  public void join(int[][] childMatrix, int[][] parentMatrix, 
                     int fromIndex, int toIndex) {
    for (int i1=0, i2=fromIndex; i1 < childMatrix.length; i1++, i2++)
      for (int j1=0, j2=toIndex; j1 < childMatrix.length; j1++, j2++)
        parentMatrix[i2][j2] = childMatrix[i1][j1];
  }

  // method to read matrix elements as input
  public int[][] readMatrix(int[][] temp) {
    for (int i = 0; i < temp.length; i++) {
      for (int j = 0; j < temp[0].length; j++) {
        // read matrix elements
        temp[i][j] = scan.nextInt();
      }
    }
    return temp;
  }

  // main method
  public static void main(String[] args) {

    System.out.println("Strassen Multiplication Algorithm Test\n");

    // Create an object of Matrix class
    Matrix mtx = new Matrix();

    // declare variables
    int size = 0;
    int a[][] = null; // first matrix
    int b[][] = null; // second matrix
    int c[][] = null; // resultant matrix

    System.out.print("Enter Matrix Order: ");
    size = scan.nextInt();

    // initialize matrices
    a = new int[size][size];
    b = new int[size][size];
    c = new int[size][size];

    // read matrix A and B
    System.out.println("Enter Matrix A: ");
    a = mtx.readMatrix(a);
    System.out.println("Enter Matrix B: ");
    b = mtx.readMatrix(b);

    // multiplication of matrix
    c = mtx.multiply(a, b);

    // display resultant matrix
    System.out.println("Resultant Matrix: ");
    for(int i=0; i<c.length; i++) {
      for(int j=0; j<c[0].length; j++) {
        System.out.print(c[i][j]+" ");
      }
      System.out.println(); // new line
    }
  }
}

Output for different test-cases:-

Strassen Multiplication Algorithm Test

Enter Matrix Order: 2
Enter Matrix A:
1 3
7 5
Enter Matrix B:
6 8
4 2
Resultant Matrix:
18 14
62 66

Strassen Multiplication Algorithm Test

Enter Matrix Order: 4
Enter Matrix A:
5 2 6 1
0 6 2 0
3 8 1 4
1 8 5 6
Enter Matrix B:
7 5 8 0
1 8 2 6
9 4 3 8
5 3 7 9
Resultant Matrix:
96 68 69 69
24 56 18 52
58 95 71 92
90 107 81 142

Time complexity = O(n log 7/2) = O(n^2.8074)

The O(n^2.8074) is slightly lesser than O(n³) but this method is usually not preferred for practical purposes.

The constants used in Strassen’s method are high and most of the time the first basic method works better. To find multiplication of Sparse matrices (which contains very few non-zero elements) better algorithms are available. The submatrices in recursion take extra space. Because of the limited precision of computer arithmetic on noninteger values, larger errors accumulate in Strassen’s algorithm than in the first basic method.

See more matrix programs in Java:- 

1. Program to Print 3×3 Matrix 
2. Sum of matrix elements in Java
3. Sum of Diagonal Elements of Matrix in Java 
4. Row sum and Column sum of Matrix in Java
5. Matrix Addition in Java
6. Subtraction of two matrices in Java 
7. Transpose of a Matrix in Java 
8. Menu-driven program for Matrix operations

If you enjoyed this post, share it with your friends. Do you want to share more information about the topic discussed above or do you find anything incorrect? Let us know in the comments. Thank you!